

Calculations Using the First Order Rate Equation: r kN. This graph shows the pattern of the decay. Determination of the Time to Decay Determination and Use of the Half-Life. Notice that they halve after every half-life. This diagram shows the parent atoms only. You can’t tell when a green will turn into a red, or which green will decay, but after every half-life, half of the green parents will have decayed into red daughters. They decay into the red squares – the daughter nuclei. In this decay model, the green squares represent the parent unstable nuclei. Half life formula By using the following decay formula, the number of unstable nuclei in a radioactive element left after t can be calculated: N ( t ) N 0 × 0. The term is most commonly used in relation to atoms undergoing radioactive decay, but can be used to describe other types of decay, whether exponential or not. Working out the half-life allows us to calculate when a radioactive element will become stable. Half-life is defined as the amount of time it takes a given quantity to decrease to half of its initial value. Although radioactive decay is a random process, statistically, over a time called the half-life, half of the parent radioactive nuclei will have decayed. This process is called radioactive decay. With half-life in B1 and the start value in B2 (which is really for Day 0), then put days 1, 2, 3 etc.
#Half life formula license#
Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License 4.0 license.When an unstable nucleus gives out an alpha or beta particle, the nucleus turns into the nucleus of a new element. We recommend using aĪuthors: Gilbert Strang, Edwin “Jed” Herman Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, In calculations of radioactivity one of two parameters (decay constant or half-life), which characterize the rate of decay, must be known. Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format,

Want to cite, share, or modify this book? This book isĬreative Commons Attribution-NonCommercial-ShareAlike License 4.0 Notice that in an exponential growth model, we have These systems follow a model of the form y = y 0 e k t, y = y 0 e k t, where y 0 y 0 represents the initial state of the system and k k is a positive constant, called the growth constant. In this section, we examine exponential growth and decay in the context of some of these applications. Indium-112 has a half life of 14.4 minutes.
#Half life formula how to#
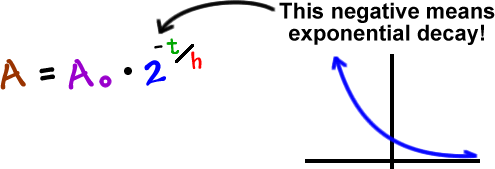
Taking the natural logarithm of both sides, we get: and so, How to Calculate Half Life. We start with, After a time, the number of radioactive nuclei halves. The following tools can generate any one of the values from the other three in the half-life formula for a substance undergoing decay to decrease by half. Similarly, the elapsed time t and the initial quantity N (0) of a radioactive isotope can also be calculated by following the same process. We will now derive a formula to get the half life from the decay constant. From population growth and continuously compounded interest to radioactive decay and Newton’s law of cooling, exponential functions are ubiquitous in nature. A radioactive isotope will remain 15.625 grams after 30 years if its half-life is 6 years, and initial values are 500 grams. Exponential growth and decay show up in a host of natural applications. The formula for half life calculations is: NtN0(1/2)(t/t(1/2)) or NtN0/2(t/t(1/2) or NtN0 2(-t/t(1/2) Where Nt is how much of the substance you have left at time t N0 is how much you started with (at time 0) t is how much time has elepsed, and t(1/2) is the half life of the substance. One of the most prevalent applications of exponential functions involves growth and decay models.
2.8.3 Use the exponential decay model in applications, including radioactive decay and Newton’s law of cooling.2.8.2 Explain the concept of doubling time.

The measurement of this quantity may take place in grams, moles, number of atoms, etc. Where, N0 refers to the initial quantity of the substance that will decay. the formula which calculates the half life is, N(t) N0e-t ln(2)/t1/2.


 0 kommentar(er)
0 kommentar(er)
